Constructing binary axes¶
Unlike many sociological concepts, “community” isn’t obviously one side of a binary distinction. I explore here whether binary embedding axes can be usefully constructed and applied to the concept of community. I choose to do so because binary concepts are pervasive in the social sciences, and because binary axes are one of the main conceptual and methodological contributions social scientists have made to the study of embeddings (starting with Kozlowski et al 2019).
Binaries are pervasive. While social structures like class and gender can divide the world into more than two categories, they can also orient social life along binary axes: rich-poor, masculine-feminine, etc. Indeed, Durkheim argues that the sacred-profane binary is fundamental to the social act of classification in general.
But what’s the opposite of community? Social scientist and social actors write and talk about lack, or loss, or absence, without necessarily giving it a name of its own. Again, Durkheim lurks here, when he distinguishes between lack of integration and lack of regulation. The latter is anomie, but what’s the former? Egoism? Individualism? I’m not sure that’s a fruitful path to explore, though it might be.
Instead of Durkheim, I’ll turn to Tönnies, and explore the distinction between “community” and “society”. The basic method for constructing a binary axis from word vectors is this is this:
create an axis from a single pair, by subtraction
create an axis from multiple pairs, by averaging
I don’t know of obvious synonyms for either “community” or “society” to construct multiple pairs with, so I’ll start with that single pair here. But based on my prior exploration of words similar to community, I suspect a “local” - “global” axis might be correlated with the “community” - “society” one.
Like Kozlowski et al, I might plot where various other words fall relative to this community-society axis. What series of words should I pick to compare? A list of abstract social science concepts would be nice. Since I don’t have that, I’ll start by just going over the whole vocabulary and list words that are nearest one pole or the other. Would that then would work to construct pairs for axis expansion?
Conversely, I might plot where “community” and related words fall on another axis, like the local-global one – or even axes related to class, gender, morality, etc that prior papers have used. This would be akin to what Arseniev-Koehler and Foster do for fatness.
Notes on prior methods and code¶
CMDist package (Stoltz and Taylor 2019)¶
https://github.com/dustinstoltz/CMDist/blob/master/R/get_relations.R
CMDist includes examples of averaging concepts - which differs from their method for creating a multiple-word pseudo-document. get_direction() and get_centroid() are the functions to look at.
CMDist implements 3 versions for binary axes in get_direction():
difference then average (Kozlowski et al)
average then difference
Euclidean norm (How is this different from Kozlowski et al? Don’t they norm in their original code? This method comes from the Bolukbási et al paper that the whatlies package also references, so hopefully they’re doing the same thing.)
Geometry of Culture (Kozlowski et al 2019)¶
https://github.com/KnowledgeLab/GeometryofCulture/blob/master/code/build_cultural_dimensions.R
This is what the Geometry of Culture code does:
norm each vector (divide by sqrt(sum(x^2)), the l2-norm)
take differences between pairs
norm again
take average of difference vectors
norm again
Machine learning / cultural learning (Arseniev-Koehler and Foster 2020)¶
https://github.com/arsena-k/Word2Vec-bias-extraction/blob/master/dimension.py
https://github.com/arsena-k/Word2Vec-bias-extraction/blob/master/build_lexicon.py
whatlies package (Warmerdam et al 2020)¶
The whatlies package is a new tool from the NLP company RASA. It’s meant to provide a consistent way to explore, manipulate, and visualize embeddings from different sources. How similar is the vector algebra outlined in the papers I describe above to the methods used and demoed in the whatlies package? Can I use tools from whatlies to implement those methods, or something close enough?
The advantage of using whatlies over gensim seems to be that the result of whatever vector algebra remains either an EmbeddingSet or an Embedding, which makes it easier to calculate similarities, plot projections, etc., downstream. I think gensim might involve more low-level fiddling with numpy arrays, but the same things could be done.
Most of the relevant methods live in the EmbeddingSet class, not the Embedding class.
There’s a transformer to normalize an EmbeddingSet: https://github.com/RasaHQ/whatlies/blob/master/whatlies/transformers/_normalizer.py#L8
Subtraction is implemented for individual Embeddings, but division isn’t, so norming without using an EmbeddingSet and transformer isn’t possible.
There’s also method to take the average of an embedding set, with could be done with a set of differences. https://github.com/RasaHQ/whatlies/blob/master/whatlies/embeddingset.py#L523
The from_names_X() method provides a way to turn something like gensim KeyedVectors into an EmbeddingSet directly, without saving the vectors to a file and loading them as a GensimLanguage object. (The GensimLanguage object doesn’t necessarily have all the same methods? I’m unsure which way is better.) https://github.com/RasaHQ/whatlies/blob/master/whatlies/embeddingset.py#L328
I also now understand that the default metric for plot_interactive() isn’t cosine similarity or cosine distance; it’s normalized scalar projection, which they represent as the > operator.
https://github.com/RasaHQ/whatlies/blob/master/whatlies/embeddingset.py#L1119
https://github.com/RasaHQ/whatlies/blob/master/whatlies/embedding.py#L115
I’m not convinced that the interactive scatterplots I make here are the clearest way to show my findings, but they’re a starting point.
Other papers and packages¶
Waller and Anderson 2020 have an interesting method of constructing and expanding binary axes for community embeddings based on pairs of subreddits, but I couldn’t find any of their code posted publicly.
In gensim, .init_sims() norms vectors. That method will be replaced by .fill_norms() when gensim 4.0.0 is available, but that version is still in beta as of now (https://github.com/RaRe-Technologies/gensim/releases).
A note on English and other languages¶
I’m doing my main analysis in English. To understand the limits of my analysis, I might think a bit about how Anglocentric the concept of “community” might be.
Based on Benedict Anderson’s discussion of the international translations of his book Imagined Communities, I have reason to think that “community” doesn’t necessarily translate well into a language like French. Communautarisme, I’ve heard, has something of a negative connotation.
Tönnies, however, was writing about community in German, which is to say he was really writing about Gemeinschaft. English-speaking sociologists sometimes use that word, Gemeinschaft, to emphasize and invoke a moral, resonant experience of community. So it might be interesting to find or train German-language word embeddings and construct a Gemeinschaft-Gesellschaft axis for comparison. An ambitious extension would be to train a model on Tönnies’s work and see how that model looked similar or different.
A few sources for pretrained German-language word vectors:
(I wish these pages had more metadata about when the models were trained and posted online.)
Text of Tönnies, Gemeinschaft und Gesellschaft (1887 edition):
Load packages and embeddings¶
# load packages
import os
import gensim.downloader as api
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import altair as alt
from whatlies import Embedding, EmbeddingSet
from whatlies.language import GensimLanguage
from whatlies.transformers import Normalizer
# set up figures so the resolution is sharper
# borrowed from https://blakeaw.github.io/2020-05-25-improve-matplotlib-notebook-inline-res/
sns.set(rc={"figure.dpi":100, 'savefig.dpi':300})
sns.set_context('notebook')
sns.set_style("darkgrid")
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('retina')
# borrowed from https://github.com/altair-viz/altair/issues/1021
def my_theme(*args, **kwargs):
return {'width': 500, 'height': 400}
alt.themes.register('my-chart', my_theme)
alt.themes.enable('my-chart')
ThemeRegistry.enable('my-chart')
# load gensim vectors (as KeyedVectors)
wv_wiki = api.load("glove-wiki-gigaword-200")
if not os.path.isfile("glove-wiki-gigaword-200.kv"):
wv_wiki.save("glove-wiki-gigaword-200.kv")
# load vectors as whatlies GensimLanguage
lang_wiki = GensimLanguage("glove-wiki-gigaword-200.kv")
# load vectors as whatlies EmbeddingSet
emb_wiki = EmbeddingSet.from_names_X(names=wv_wiki.index2word,
X=wv_wiki.vectors)
What’s the advantage of using GensimLanguage anyway? Is it faster or more efficient? It’s annoying to have to write out the vectors after you load them. (More annoying for a model you’ve trained yourself, I’d imagine.)
Community - society dimension¶
# subtraction and averaging with gensim
wv_wiki['community'] - wv_wiki['society']
array([ 0.21125801, -0.20572 , 0.25577 , -1.07679 , -0.5692 ,
0.02297999, 0.21760401, -0.020017 , -1.2587 , 0.041086 ,
-0.218533 , -0.12349999, 0.411472 , 0.141909 , 0.19098002,
-0.421192 , 0.012209 , -0.05559 , 0.03202 , 0.61028904,
-0.65889 , 0.5112002 , -0.38690004, -0.02410999, 0.52295 ,
-0.19727 , 0.11050999, 0.30345 , 0.175234 , -0.6936 ,
-1.3031931 , -0.54581 , -0.37711 , 0.052096 , 0.251908 ,
-0.732768 , -0.37988997, -0.08363 , -0.28567997, 0.241564 ,
-0.02117001, 0.13353002, -0.08291 , -0.22328001, 0.10966 ,
0.33075 , -0.43351 , -0.06479999, -0.545506 , 0.07736999,
0.725142 , -0.801156 , -0.11023 , 0.153733 , 0.26353002,
-0.06733999, -0.172911 , -0.49693003, -0.02404001, 0.19105 ,
0.13389 , -0.21914999, 0.03555 , 0.39821002, -0.23501399,
-0.09658003, -1.01461 , 0.01980007, 0.52537 , -0.66896 ,
-0.228967 , 0.7949 , -0.39415997, -0.580275 , 0.22458 ,
-0.02671 , -0.438312 , -0.175468 , 0.45229098, 0.19266999,
0.44222 , 0.43056 , 0.2129 , 0.17333 , -0.16205001,
-0.22395003, -0.27346998, -0.03958 , -0.69710004, -0.16941 ,
0.12035 , 0.11173001, -0.53375995, -0.32883 , -0.00563 ,
0.06819 , -0.099357 , -0.323266 , 0.01810001, -0.32955799,
-0.12631997, -0.08148001, -0.367723 , 0.13514999, -0.326734 ,
-0.13970995, -0.104549 , 0.35557002, -0.50458 , 0.152675 ,
-0.50527 , 0.29231 , -0.14010699, -0.31751102, -0.13655901,
-0.124451 , 0.08310997, -0.86984 , 0.11697999, -0.25719398,
0.08576001, -0.01467001, 0.67732 , 0.03302525, 0.132038 ,
-0.17480999, 0.46077 , -0.37312 , 0.41101003, 0.425044 ,
0.085655 , -0.4317 , 0.12938002, -0.003296 , 0.081862 ,
0.33249998, -0.27705002, -0.27912 , -0.513407 , 0.12053001,
-0.84422004, -0.38838 , 0.24156001, 1.0012801 , 0.33923 ,
-0.179914 , 0.083 , -0.16885 , 0.06496 , -0.17139998,
-0.29468998, -0.240162 , -0.09658001, 0.466917 , 0.52645 ,
0.34828 , -0.350604 , -0.241685 , 0.527246 , -0.47434 ,
-0.080662 , 0.15636 , 0.145862 , 0.34217098, 0.97707 ,
0.6603 , 0.30905002, 0.19642001, 0.06003001, 0.10062999,
-0.5082 , -0.769381 , 0.01367 , 0.0382276 , 0.65116 ,
-1.07669 , 0.68782 , 0.27273 , -0.10385001, -0.6333 ,
-0.89898 , 0.948482 , 0.032346 , 0.12616 , 0.63309 ,
0.47342 , 0.00784 , -0.35312 , -0.410943 , 0.41627002,
0.162112 , -0.39482 , -0.380659 , 0.07424 , -0.34482002,
-0.30944 , -0.289902 , -0.39461 , -0.29156 , -0.75926 ],
dtype=float32)
# subtraction and averaging with whatlies
diff = emb_wiki["community"] - emb_wiki["society"]
# what's nice is that this is an Embedding object too
diff
Emb[(community - society)]
diff.vector
array([ 0.21125801, -0.20572 , 0.25577 , -1.07679 , -0.5692 ,
0.02297999, 0.21760401, -0.020017 , -1.2587 , 0.041086 ,
-0.218533 , -0.12349999, 0.411472 , 0.141909 , 0.19098002,
-0.421192 , 0.012209 , -0.05559 , 0.03202 , 0.61028904,
-0.65889 , 0.5112002 , -0.38690004, -0.02410999, 0.52295 ,
-0.19727 , 0.11050999, 0.30345 , 0.175234 , -0.6936 ,
-1.3031931 , -0.54581 , -0.37711 , 0.052096 , 0.251908 ,
-0.732768 , -0.37988997, -0.08363 , -0.28567997, 0.241564 ,
-0.02117001, 0.13353002, -0.08291 , -0.22328001, 0.10966 ,
0.33075 , -0.43351 , -0.06479999, -0.545506 , 0.07736999,
0.725142 , -0.801156 , -0.11023 , 0.153733 , 0.26353002,
-0.06733999, -0.172911 , -0.49693003, -0.02404001, 0.19105 ,
0.13389 , -0.21914999, 0.03555 , 0.39821002, -0.23501399,
-0.09658003, -1.01461 , 0.01980007, 0.52537 , -0.66896 ,
-0.228967 , 0.7949 , -0.39415997, -0.580275 , 0.22458 ,
-0.02671 , -0.438312 , -0.175468 , 0.45229098, 0.19266999,
0.44222 , 0.43056 , 0.2129 , 0.17333 , -0.16205001,
-0.22395003, -0.27346998, -0.03958 , -0.69710004, -0.16941 ,
0.12035 , 0.11173001, -0.53375995, -0.32883 , -0.00563 ,
0.06819 , -0.099357 , -0.323266 , 0.01810001, -0.32955799,
-0.12631997, -0.08148001, -0.367723 , 0.13514999, -0.326734 ,
-0.13970995, -0.104549 , 0.35557002, -0.50458 , 0.152675 ,
-0.50527 , 0.29231 , -0.14010699, -0.31751102, -0.13655901,
-0.124451 , 0.08310997, -0.86984 , 0.11697999, -0.25719398,
0.08576001, -0.01467001, 0.67732 , 0.03302525, 0.132038 ,
-0.17480999, 0.46077 , -0.37312 , 0.41101003, 0.425044 ,
0.085655 , -0.4317 , 0.12938002, -0.003296 , 0.081862 ,
0.33249998, -0.27705002, -0.27912 , -0.513407 , 0.12053001,
-0.84422004, -0.38838 , 0.24156001, 1.0012801 , 0.33923 ,
-0.179914 , 0.083 , -0.16885 , 0.06496 , -0.17139998,
-0.29468998, -0.240162 , -0.09658001, 0.466917 , 0.52645 ,
0.34828 , -0.350604 , -0.241685 , 0.527246 , -0.47434 ,
-0.080662 , 0.15636 , 0.145862 , 0.34217098, 0.97707 ,
0.6603 , 0.30905002, 0.19642001, 0.06003001, 0.10062999,
-0.5082 , -0.769381 , 0.01367 , 0.0382276 , 0.65116 ,
-1.07669 , 0.68782 , 0.27273 , -0.10385001, -0.6333 ,
-0.89898 , 0.948482 , 0.032346 , 0.12616 , 0.63309 ,
0.47342 , 0.00784 , -0.35312 , -0.410943 , 0.41627002,
0.162112 , -0.39482 , -0.380659 , 0.07424 , -0.34482002,
-0.30944 , -0.289902 , -0.39461 , -0.29156 , -0.75926 ],
dtype=float32)
gensim and whatlies are doing the same thing — that’s good!
The methods I researched above make it sound like normalizing the vectors is an important part of the process, so I explore how to do that next.
# this is the numpy default and almost certainly not what I want
diff.norm
5.8058085
# this is the l2 norm, which *is* what I want
diff_norm = EmbeddingSet(diff).transform(Normalizer(norm='l2'))
diff_norm['(community - society)']
Emb[(community - society)]
Now I compare similarity scores for the raw and normalized binary axis vectors.
# toward the "community" end of the axis
emb_wiki.score_similar(diff)
[(Emb[modding], 0.589404284954071),
(Emb[community], 0.595145583152771),
(Emb[master-planned], 0.614898145198822),
(Emb[unincorporated], 0.6228582262992859),
(Emb[baraki], 0.6278692483901978),
(Emb[mixed-income], 0.6375738382339478),
(Emb[homa], 0.6425093412399292),
(Emb[communities], 0.6557735204696655),
(Emb[clarkston], 0.6563817262649536),
(Emb[mechanicsville], 0.6569202542304993)]
# toward the "society" end
emb_wiki.score_similar(-diff)
[(Emb[society], 0.5049312710762024),
(Emb[microscopical], 0.5116949081420898),
(Emb[cymmrodorion], 0.5465895533561707),
(Emb[meteoritical], 0.5658960342407227),
(Emb[linnean], 0.579145610332489),
(Emb[ophthalmological], 0.5990228652954102),
(Emb[anti-vivisection], 0.5998556613922119),
(Emb[entomological], 0.6023805141448975),
(Emb[dilettanti], 0.6036361455917358),
(Emb[speleological], 0.6155304908752441)]
emb_wiki_norm = emb_wiki.transform(Normalizer(norm='l2'))
emb_wiki_norm.score_similar(diff_norm['(community - society)'])
[(Emb[modding], 0.589404284954071),
(Emb[community], 0.595145583152771),
(Emb[master-planned], 0.614898145198822),
(Emb[unincorporated], 0.6228581666946411),
(Emb[baraki], 0.6278692483901978),
(Emb[mixed-income], 0.6375738382339478),
(Emb[homa], 0.6425093412399292),
(Emb[communities], 0.6557735204696655),
(Emb[clarkston], 0.6563817262649536),
(Emb[mechanicsville], 0.6569201946258545)]
That’s … reassuring? that the metrics are exactly the same. I’ll use the raw vectors here, for simplicity. But norming probably matters when averaging is involved.
Next, I’ll explore similarity to each end of the community-society axis across the entire vocabulary.
sim_diff = emb_wiki.score_similar(diff, n=len(emb_wiki), metric='cosine')
sim_diff[0:100]
[(Emb[modding], 0.589404284954071),
(Emb[community], 0.595145583152771),
(Emb[master-planned], 0.614898145198822),
(Emb[unincorporated], 0.6228582262992859),
(Emb[baraki], 0.6278692483901978),
(Emb[mixed-income], 0.6375738382339478),
(Emb[homa], 0.6425093412399292),
(Emb[communities], 0.6557735204696655),
(Emb[clarkston], 0.6563817262649536),
(Emb[mechanicsville], 0.6569202542304993),
(Emb[gated], 0.6586361527442932),
(Emb[neighborhood], 0.662484884262085),
(Emb[cybersitter], 0.6649418473243713),
(Emb[mixed-use], 0.6691757440567017),
(Emb[taizé], 0.6723114252090454),
(Emb[har], 0.6735500693321228),
(Emb[pittsylvania], 0.6744325160980225),
(Emb[age-restricted], 0.6762539148330688),
(Emb[conroe], 0.6776710748672485),
(Emb[leflore], 0.6826707124710083),
(Emb[mahru], 0.6833871603012085),
(Emb[neighbourhood], 0.6848275661468506),
(Emb[rossmoor], 0.6849431991577148),
(Emb[perushim], 0.6870222687721252),
(Emb[taize], 0.6876176595687866),
(Emb[viejo], 0.688064694404602),
(Emb[etzion], 0.6894879341125488),
(Emb[washtenaw], 0.6914564967155457),
(Emb[haasara], 0.6928879618644714),
(Emb[vado], 0.6929028034210205),
(Emb[pagemill], 0.6935604810714722),
(Emb[silwan], 0.6948147416114807),
(Emb[village], 0.6956229209899902),
(Emb[zaz-e], 0.6958953738212585),
(Emb[merced], 0.6982126832008362),
(Emb[cyberpatrol], 0.7004590034484863),
(Emb[kakavand], 0.7008499503135681),
(Emb[transmitter], 0.7009164690971375),
(Emb[94596], 0.7016159296035767),
(Emb[livejournal], 0.7019829154014587),
(Emb[zionsville], 0.7031553983688354),
(Emb[blears], 0.703620195388794),
(Emb[palmdale], 0.7037292122840881),
(Emb[cottonwood], 0.7040864825248718),
(Emb[hanza], 0.7044801712036133),
(Emb[muran], 0.7045321464538574),
(Emb[mirik], 0.705109179019928),
(Emb[14-nation], 0.7056152820587158),
(Emb[chemeketa], 0.7059245705604553),
(Emb[residential], 0.7060489654541016),
(Emb[centerville], 0.7063371539115906),
(Emb[shirgah], 0.706989586353302),
(Emb[shavur], 0.7071289420127869),
(Emb[zagheh], 0.7074677348136902),
(Emb[adamsville], 0.7076104879379272),
(Emb[outreach], 0.7086617946624756),
(Emb[dastgerdan], 0.7091307044029236),
(Emb[akhtachi-ye], 0.7092592716217041),
(Emb[ringmer], 0.709490954875946),
(Emb[off-campus], 0.7105263471603394),
(Emb[clackamas], 0.7107102870941162),
(Emb[rudboneh], 0.7111980319023132),
(Emb[summerhaven], 0.711326003074646),
(Emb[semi-rural], 0.7116978764533997),
(Emb[lakewood], 0.712110161781311),
(Emb[aliso], 0.7124844789505005),
(Emb[aubusson], 0.7124911546707153),
(Emb[mangur-e], 0.7125020623207092),
(Emb[manj], 0.7125272154808044),
(Emb[briceville], 0.7126100659370422),
(Emb[kiryas], 0.7131937146186829),
(Emb[low-income], 0.7132914662361145),
(Emb[creek], 0.7134579420089722),
(Emb[abobo], 0.7138109803199768),
(Emb[charuymaq-e], 0.7140942215919495),
(Emb[netiv], 0.7151552438735962),
(Emb[parisyan], 0.7156028747558594),
(Emb[dellums], 0.7157094478607178),
(Emb[gali], 0.716493546962738),
(Emb[dam], 0.7165515422821045),
(Emb[kristang], 0.7168752551078796),
(Emb[garmkhan], 0.7168968319892883),
(Emb[littleover], 0.7169832587242126),
(Emb[6,500], 0.7176810503005981),
(Emb[makoko], 0.7182502150535583),
(Emb[neighborhoods], 0.7185196876525879),
(Emb[sanabis], 0.7185332179069519),
(Emb[cibecue], 0.7186675667762756),
(Emb[right-to-know], 0.7191548347473145),
(Emb[contai], 0.7199649810791016),
(Emb[anthonis], 0.7201418876647949),
(Emb[santee], 0.7206466794013977),
(Emb[upland], 0.7207662463188171),
(Emb[municipality], 0.7207773923873901),
(Emb[shusef], 0.7210158109664917),
(Emb[comarca], 0.7211617231369019),
(Emb[pinyon-juniper], 0.7212787866592407),
(Emb[villages], 0.7215777635574341),
(Emb[slatina], 0.721792995929718),
(Emb[kojur], 0.72184157371521)]
sim_diff[-100:]
[(Emb[kautilya], 1.3038641214370728),
(Emb[gynaecological], 1.303879737854004),
(Emb[physikalische], 1.3040287494659424),
(Emb[silurians], 1.3041560649871826),
(Emb[soerensen], 1.3042516708374023),
(Emb[honus], 1.304616928100586),
(Emb[xiaokang], 1.304952621459961),
(Emb[genootschap], 1.305346131324768),
(Emb[fleischner], 1.305643081665039),
(Emb[academician], 1.3060909509658813),
(Emb[ichthyologists], 1.3062193393707275),
(Emb[idsa], 1.3071272373199463),
(Emb[ethnological], 1.30740487575531),
(Emb[teratology], 1.3079063892364502),
(Emb[f.r.s.], 1.3086650371551514),
(Emb[saint-jean-baptiste], 1.3093072175979614),
(Emb[fruitbearing], 1.3098504543304443),
(Emb[anatomy], 1.3098732233047485),
(Emb[feudalist], 1.3105204105377197),
(Emb[mycological], 1.3109546899795532),
(Emb[gulbarg], 1.3126049041748047),
(Emb[bnhs], 1.313199758529663),
(Emb[mammalogists], 1.313377857208252),
(Emb[neurochemistry], 1.3137081861495972),
(Emb[matriarchal], 1.3138256072998047),
(Emb[decadence], 1.3145842552185059),
(Emb[theosophical], 1.3147900104522705),
(Emb[cpic], 1.3152551651000977),
(Emb[roentgen], 1.3159534931182861),
(Emb[numismatic], 1.316864252090454),
(Emb[astronautical], 1.316948413848877),
(Emb[kisfaludy], 1.31697678565979),
(Emb[ncnp], 1.3169808387756348),
(Emb[feudalistic], 1.317538857460022),
(Emb[anti-slavery], 1.317636489868164),
(Emb[chirurgical], 1.3178396224975586),
(Emb[dialectic], 1.3181957006454468),
(Emb[gynaecologists], 1.3191827535629272),
(Emb[rospa], 1.3197741508483887),
(Emb[lepidopterists], 1.3204152584075928),
(Emb[görres], 1.3209925889968872),
(Emb[bibliographical], 1.3217389583587646),
(Emb[gerontological], 1.3217589855194092),
(Emb[columbian], 1.3243486881256104),
(Emb[arniko], 1.3261610269546509),
(Emb[throwaways], 1.3266232013702393),
(Emb[cuirassier], 1.329356074333191),
(Emb[cinematographers], 1.3297762870788574),
(Emb[apothecaries], 1.3303970098495483),
(Emb[cashless], 1.3320657014846802),
(Emb[crcs], 1.3322489261627197),
(Emb[non-resistance], 1.333126425743103),
(Emb[psychical], 1.3336145877838135),
(Emb[inverts], 1.334222674369812),
(Emb[philatelic], 1.334324598312378),
(Emb[musicological], 1.3355190753936768),
(Emb[horological], 1.3357938528060913),
(Emb[watercolour], 1.3358557224273682),
(Emb[rspca], 1.3360782861709595),
(Emb[anarcho-capitalist], 1.338468313217163),
(Emb[psychoanalytical], 1.33878493309021),
(Emb[new-york], 1.341145396232605),
(Emb[illustrators], 1.341640591621399),
(Emb[malacological], 1.345167875289917),
(Emb[nedlloyd], 1.345234751701355),
(Emb[pelerin], 1.3458216190338135),
(Emb[asiatic], 1.3465323448181152),
(Emb[societies], 1.3467721939086914),
(Emb[demutualised], 1.3468401432037354),
(Emb[classless], 1.34755539894104),
(Emb[riksmål], 1.347561240196228),
(Emb[mythopoeic], 1.3492627143859863),
(Emb[phrenological], 1.3511271476745605),
(Emb[prosvita], 1.3549458980560303),
(Emb[antiquaries], 1.357465147972107),
(Emb[dermatologic], 1.3581734895706177),
(Emb[etchers], 1.3585529327392578),
(Emb[archæological], 1.3601726293563843),
(Emb[vivisection], 1.3617887496948242),
(Emb[manumission], 1.363285779953003),
(Emb[aspca], 1.363932490348816),
(Emb[kle], 1.3672311305999756),
(Emb[vidocq], 1.3676127195358276),
(Emb[philomathean], 1.368377685546875),
(Emb[krcs], 1.372873067855835),
(Emb[ecclesiological], 1.3750007152557373),
(Emb[hakluyt], 1.3761779069900513),
(Emb[mattachine], 1.3781378269195557),
(Emb[herpetological], 1.3806662559509277),
(Emb[gesellschaft], 1.3832592964172363),
(Emb[speleological], 1.3844695091247559),
(Emb[dilettanti], 1.3963638544082642),
(Emb[entomological], 1.3976194858551025),
(Emb[anti-vivisection], 1.400144338607788),
(Emb[ophthalmological], 1.4009771347045898),
(Emb[linnean], 1.4208543300628662),
(Emb[meteoritical], 1.4341039657592773),
(Emb[cymmrodorion], 1.4534103870391846),
(Emb[microscopical], 1.4883050918579102),
(Emb[society], 1.4950687885284424)]
These results make sense, but there’s a downside to using all 400,000 words in the vocabulary - it means that a lot of rare words are included. That’s why you see things like “Mattachine Society” or “Linnean Society”.
Briefly, I’ll look at the words in the middle of the list.
sim_diff[len(sim_diff)//2 - 50 : len(sim_diff)//2 + 50]
[(Emb[drolet], 1.000519871711731),
(Emb[109,500], 1.0005199909210205),
(Emb[http://www.nytsyn.com], 1.0005203485488892),
(Emb[kloeden], 1.0005204677581787),
(Emb[fita], 1.000520944595337),
(Emb[27.19], 1.0005214214324951),
(Emb[zohur], 1.0005216598510742),
(Emb[maierhofer], 1.0005218982696533),
(Emb[suff], 1.0005223751068115),
(Emb[2,928], 1.000523567199707),
(Emb[untidiness], 1.0005238056182861),
(Emb[single-sideband], 1.0005238056182861),
(Emb[kumiko], 1.0005241632461548),
(Emb[finds], 1.0005241632461548),
(Emb[visionics], 1.0005242824554443),
(Emb[horwell], 1.0005242824554443),
(Emb[anti-globalisation], 1.0005245208740234),
(Emb[hoshangabad], 1.0005253553390503),
(Emb[o'donnells], 1.0005265474319458),
(Emb[logjammed], 1.0005278587341309),
(Emb[vissel], 1.0005289316177368),
(Emb[clínica], 1.0005289316177368),
(Emb[nguyên], 1.0005310773849487),
(Emb[maheswaran], 1.0005319118499756),
(Emb[inauthenticity], 1.0005319118499756),
(Emb[tziona], 1.0005320310592651),
(Emb[affective], 1.0005321502685547),
(Emb[97-year], 1.0005325078964233),
(Emb[smeg], 1.0005325078964233),
(Emb[yeshwant], 1.000532627105713),
(Emb[angophora], 1.0005327463150024),
(Emb[connacht], 1.000532865524292),
(Emb[beltransgaz], 1.0005338191986084),
(Emb[118.14], 1.0005351305007935),
(Emb[rongmei], 1.000535249710083),
(Emb[rifa], 1.0005358457565308),
(Emb[komnene], 1.0005362033843994),
(Emb[kelland], 1.0005366802215576),
(Emb[115.67], 1.0005366802215576),
(Emb[casina], 1.0005383491516113),
(Emb[forming], 1.00053870677948),
(Emb[ohlsson], 1.0005388259887695),
(Emb[ne4], 1.0005393028259277),
(Emb[hydrocortisone], 1.0005393028259277),
(Emb[bakırköy], 1.0005393028259277),
(Emb[fortin], 1.0005401372909546),
(Emb[kaukonen], 1.0005402565002441),
(Emb[mich.-based], 1.0005402565002441),
(Emb[34.77], 1.0005412101745605),
(Emb[total-goals], 1.0005412101745605),
(Emb[smethurst], 1.0005416870117188),
(Emb[stjepan], 1.000542163848877),
(Emb[xingfang], 1.0005426406860352),
(Emb[ruef], 1.000543475151062),
(Emb[airliners], 1.0005443096160889),
(Emb[www.ritzcarlton.com], 1.0005443096160889),
(Emb[interministerial], 1.0005444288253784),
(Emb[telecheck], 1.000544786453247),
(Emb[prengaman], 1.0005459785461426),
(Emb[404-526-7282], 1.0005462169647217),
(Emb[bitchy], 1.0005478858947754),
(Emb[principe], 1.000548243522644),
(Emb[undercover], 1.000549554824829),
(Emb[skyview], 1.0005497932434082),
(Emb[loker], 1.0005508661270142),
(Emb[1.2800], 1.0005518198013306),
(Emb[1.092], 1.0005518198013306),
(Emb[euro136], 1.0005526542663574),
(Emb[salmela], 1.000552773475647),
(Emb[goldenes], 1.0005537271499634),
(Emb[derail], 1.000553846359253),
(Emb[tennesee], 1.000553846359253),
(Emb[61-page], 1.0005548000335693),
(Emb[shifflett], 1.0005557537078857),
(Emb[disentis], 1.0005567073822021),
(Emb[ebina], 1.0005569458007812),
(Emb[promontories], 1.0005574226379395),
(Emb[arias], 1.000558614730835),
(Emb[yuliya], 1.000558853149414),
(Emb[cici], 1.000558853149414),
(Emb[58.79], 1.0005601644515991),
(Emb[corless], 1.0005606412887573),
(Emb[apgar], 1.0005619525909424),
(Emb[federici], 1.0005627870559692),
(Emb[unislamic], 1.0005630254745483),
(Emb[identification], 1.0005638599395752),
(Emb[t.n.t.], 1.0005638599395752),
(Emb[drager], 1.0005643367767334),
(Emb[pyrex], 1.000564694404602),
(Emb[kasauli], 1.000564694404602),
(Emb[kurnia], 1.000565528869629),
(Emb[grot], 1.0005661249160767),
(Emb[telsey], 1.0005671977996826),
(Emb[:32], 1.0005673170089722),
(Emb[shoshanna], 1.0005680322647095),
(Emb[tigrina], 1.000568151473999),
(Emb[kristoffersen], 1.0005683898925781),
(Emb[marsinah], 1.0005686283111572),
(Emb[accuracies], 1.0005710124969482),
(Emb[ogrin], 1.0005722045898438)]
That isn’t actually how you get the most orthogonal words, is it? This again helps show the issues with using the full vocabulary – many of these “words” are uncommon (e.g. names) or garbage (e.g. numbers, urls, misspellings).
The entire vocabulary isn’t terribly useful for producing more pairs of opposite words. What might I do instead?
Is there a list of just common english vocabulary in general? E.g. https://stackoverflow.com/questions/28339622/is-there-a-corpora-of-english-words-in-nltk
Ideal might be a set of common social science words. Could I approximate that that through vector averaging, using words like “community”, “society”, “sociology”, etc.? Then I could expand the set by getting a list of words most similar to that average.
To begin withh, I’ll just average “community” and “society”, to get words in the general neighborhood of both. Then I’ll use that shorter list of words as the comparison set.
avg = emb_wiki[['community', 'society']].average(name="avg(community, society)")
emb_wiki.score_similar(avg, n=100)
[(Emb[society], 0.10151195526123047),
(Emb[community], 0.1131206750869751),
(Emb[communities], 0.28810155391693115),
(Emb[societies], 0.29189276695251465),
(Emb[established], 0.3642843961715698),
(Emb[culture], 0.3817620277404785),
(Emb[social], 0.3840060234069824),
(Emb[organizations], 0.3851216435432434),
(Emb[organization], 0.3865753412246704),
(Emb[cultural], 0.4050767421722412),
(Emb[public], 0.4058724641799927),
(Emb[founded], 0.4087352752685547),
(Emb[association], 0.4117599129676819),
(Emb[institution], 0.4144657850265503),
(Emb[country], 0.42236191034317017),
(Emb[life], 0.4231107234954834),
(Emb[citizens], 0.423681378364563),
(Emb[local], 0.4252852201461792),
(Emb[part], 0.4261268377304077),
(Emb[the], 0.4262123107910156),
(Emb[education], 0.42667531967163086),
(Emb[institutions], 0.4284619092941284),
(Emb[well], 0.4290911555290222),
(Emb[member], 0.42947137355804443),
(Emb[establishment], 0.4309902787208557),
(Emb[educational], 0.4321936368942261),
(Emb[council], 0.43250930309295654),
(Emb[american], 0.43397700786590576),
(Emb[nation], 0.43632519245147705),
(Emb[national], 0.43835365772247314),
(Emb[organized], 0.44056880474090576),
(Emb[international], 0.4406183362007141),
(Emb[religious], 0.4414077401161194),
(Emb[people], 0.4478299617767334),
(Emb[which], 0.44973498582839966),
(Emb[many], 0.4502919912338257),
(Emb[youth], 0.4507424831390381),
(Emb[concerned], 0.4513043761253357),
(Emb[institute], 0.45221829414367676),
(Emb[members], 0.45271778106689453),
(Emb[arts], 0.4532017707824707),
(Emb[within], 0.4574560523033142),
(Emb[is], 0.45751142501831055),
(Emb[nonprofit], 0.45770907402038574),
(Emb[particular], 0.4583626985549927),
(Emb[foundation], 0.45936405658721924),
(Emb[now], 0.4612032175064087),
(Emb[development], 0.46199309825897217),
(Emb[leaders], 0.4629349708557129),
(Emb[and], 0.4632570743560791),
(Emb[working], 0.46432340145111084),
(Emb[growing], 0.4644703269004822),
(Emb[where], 0.46470320224761963),
(Emb[groups], 0.4647403955459595),
(Emb[interests], 0.46509718894958496),
(Emb[”], 0.465959370136261),
(Emb[nature], 0.4662094712257385),
(Emb[schools], 0.4667245149612427),
(Emb[important], 0.4682537317276001),
(Emb[united], 0.4687138795852661),
(Emb[based], 0.4693211317062378),
(Emb[today], 0.4695984721183777),
(Emb[.], 0.46967899799346924),
(Emb[recognized], 0.4700809121131897),
(Emb[population], 0.4702450633049011),
(Emb[work], 0.47040367126464844),
(Emb[leadership], 0.47093069553375244),
(Emb[scientific], 0.4716092348098755),
(Emb[organisations], 0.4717303514480591),
(Emb[non-profit], 0.47289639711380005),
(Emb[promote], 0.47300010919570923),
(Emb[associations], 0.4739416837692261),
(Emb[should], 0.4740998148918152),
(Emb[especially], 0.4744328260421753),
(Emb[lives], 0.47480159997940063),
(Emb[among], 0.4766632914543152),
(Emb[civic], 0.47673892974853516),
(Emb[living], 0.4781023859977722),
(Emb[has], 0.4785144329071045),
(Emb[both], 0.47909224033355713),
(Emb[also], 0.47925865650177),
(Emb[’s], 0.47973376512527466),
(Emb[heritage], 0.4802626967430115),
(Emb[trust], 0.480280339717865),
(Emb[way], 0.4803711771965027),
(Emb[hope], 0.48062217235565186),
(Emb[support], 0.4808751344680786),
(Emb[our], 0.48118728399276733),
(Emb[church], 0.4820277690887451),
(Emb[common], 0.48295044898986816),
(Emb[all], 0.4833552837371826),
(Emb[of], 0.4838089942932129),
(Emb[become], 0.4839017987251282),
(Emb[business], 0.4840947389602661),
(Emb[in], 0.4856555461883545),
(Emb[religion], 0.48654603958129883),
(Emb[union], 0.4866955280303955),
(Emb[science], 0.48709195852279663),
(Emb[area], 0.48812955617904663),
(Emb[families], 0.4883052706718445)]
This is an improvement. In the long run, I still should probably filter out stopwords and, uh, punctuation apparently.
sim_avg = emb_wiki.embset_similar(avg, n=100)
# quick check of norming - it still produces the same scores
(EmbeddingSet(avg, *emb_wiki)
.transform(Normalizer(norm='l2'))
.score_similar(avg, n=11))
[(Emb[avg(community, society)], 0.0),
(Emb[society], 0.1015118956565857),
(Emb[community], 0.1131206750869751),
(Emb[communities], 0.28810155391693115),
(Emb[societies], 0.29189276695251465),
(Emb[established], 0.3642843961715698),
(Emb[culture], 0.38176196813583374),
(Emb[social], 0.384006142616272),
(Emb[organizations], 0.38512158393859863),
(Emb[organization], 0.3865753412246704),
(Emb[cultural], 0.40507662296295166)]
It’s easier to plot if I have some sort of second axis, I think, even if that second axis isn’t terribly informative itself. I’ll use the average as that axis at first.
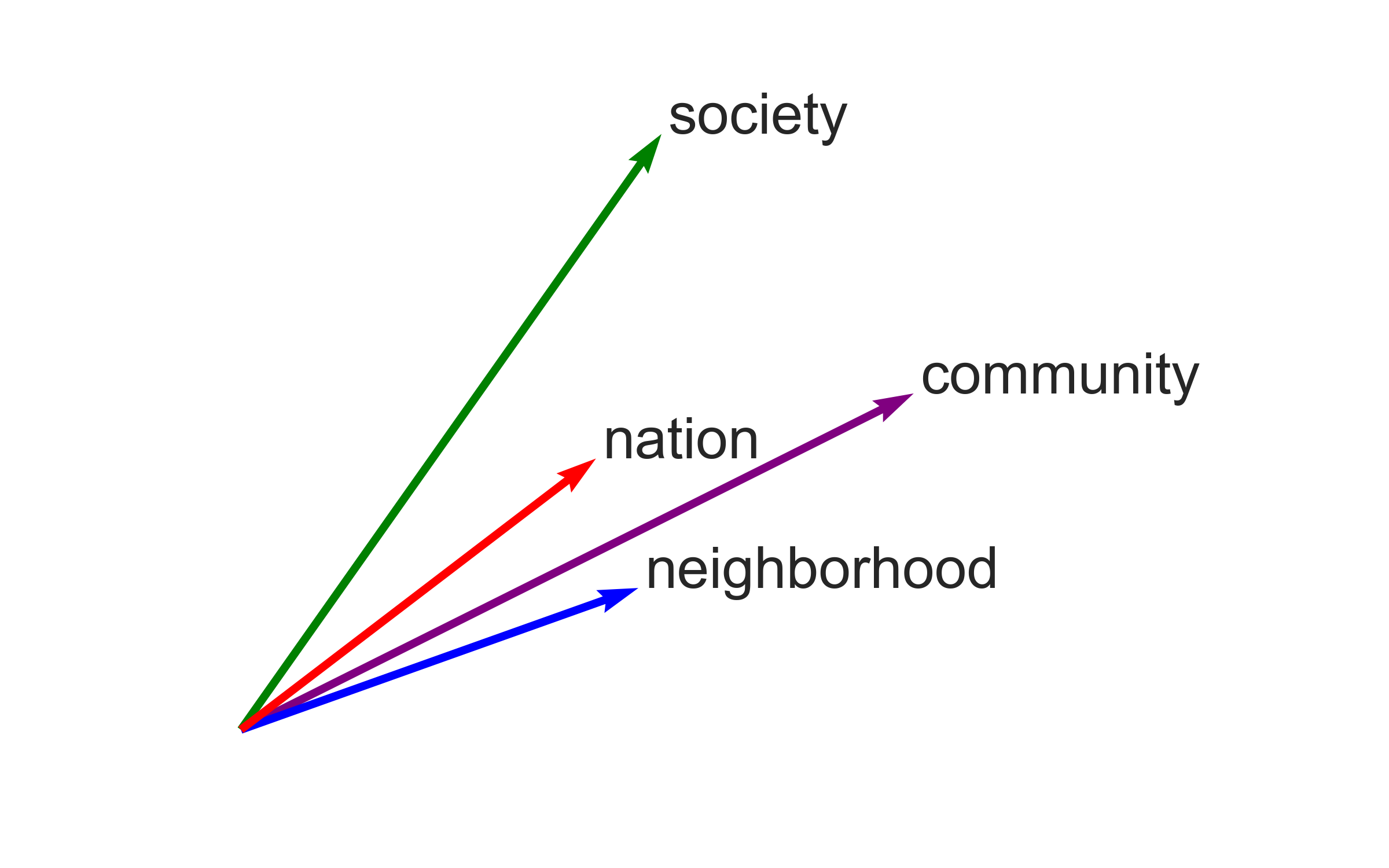
Kozlowski et al actually plot the angles of the vectors, using sports words as their comparison set. I could probably figure out how to do this eventually, but I don’t see how to immediately. Maybe that would be similar to the arrow diagrams that whatlies uses in its non-interactive plots.
# default metric - projection
sim_avg.plot_interactive(x_axis=diff, y_axis=avg)
# when cosine similarity is used, there's a clear sharp lower bound
# on the y axis, which makes sense because that's how the word set
# was defined
sim_avg.plot_interactive(x_axis=diff, y_axis=avg,
axis_metric="cosine_similarity")
# add a second binary axis, local-global
sim_avg.plot_interactive(x_axis=diff,
y_axis=emb_wiki['local'] - emb_wiki['global'])
sim_avg.plot_interactive(x_axis=diff,
y_axis=emb_wiki['local'] - emb_wiki['global'],
axis_metric='cosine_similarity')
Like Koslowski et al, I can calculate cosine similarity between the axes directly. (Note: the Embedding class has a method that does cosine distance.)
diff_loc = emb_wiki['local'] - emb_wiki['global']
diff.distance(diff_loc, metric='cosine')
0.8468398
A bigger comparison set of words might help me see more trends, but will make the plots themselves harder to read.
sim_avg2 = emb_wiki.embset_similar(avg, n=1000)
sim_avg2.plot_interactive(x_axis=diff, y_axis=avg,
axis_metric="cosine_similarity")
In fact, now words like “neighborhood” show up strongly on the “community” side of the axis.
When I explored similarity to community, I found that the most similar words to community differed between twitter- and wikipedia-based glove vectors. So, what does a comparison set look like with the twitter vectors? Are there obvious similarities and differences at a glance?
wv_twitter = api.load("glove-twitter-200")
emb_twitter = EmbeddingSet.from_names_X(names=wv_twitter.index2word,
X=wv_twitter.vectors)
diff_twitter = emb_twitter['community'] - emb_twitter['society']
avg_twitter = emb_twitter[['community', 'society']].average(name="avg(community, society)")
(emb_twitter
.embset_similar(avg_twitter, n=1000)
.plot_interactive(x_axis=diff_twitter,
y_axis=avg_twitter))
(emb_twitter
.embset_similar(avg_twitter, n=1000)
.plot_interactive(x_axis=diff_twitter,
y_axis=emb_twitter['local'] - emb_twitter['global'],
axis_metric='cosine_similarity'))
diff_loc_twitter = emb_twitter['local'] - emb_twitter['global']
diff_twitter.distance(diff_loc_twitter)
Einmal noch, auf Deutsch¶
As noted above, the sociological tradition that discusses community actually originates in German. (The French classical sociologists seem to prefer to talk about solidarité… See Aldous 1972 for a contextualization of the historical dialogue between Durkheim and Tönnies.)
Because of that origin, I’m curious about what modern German word vectors might show about Gemeinschaft (community) and Gesellschaft (society). Are there any obvious differences from English?
I’ll choose some pretrained German-language embeddings. The deepset German glove embeddings are 3.5GB, which is larger than the largest spacy model… So I’ll download that spacy model instead:
python -m spacy download de_core_news_lg
Note that I can read a little German, but I don’t know it particularly well. To make this part of the analysis more serious, actual German speakers might need to weigh in.
from whatlies.language import SpacyLanguage
emb_wiki_de = SpacyLanguage("de_core_news_lg")
diff_de = emb_wiki_de['gemeinschaft'] - emb_wiki_de['gesellschaft']
avg_de = emb_wiki_de[["gemeinschaft", "gesellschaft"]].average(name="avg(gemeinschaft, gesellschaft)")
(emb_wiki_de
.embset_similar(avg_de, n=1000)
.plot_interactive(x_axis=diff_de,
y_axis=avg_de)
.properties(width=500, height=400))
# most similar to gemeinschaft
(emb_wiki_de
.embset_similar(avg_de, n=1000)
.score_similar(diff_de, n=50))
I notice words like zusammenarbeiten, einheiten, mitglieder… Some religious words? (evangelischen, kirchlichen, konfessionelle)
# most similar to gesellschaft, as opposed to gemeinschaft
(emb_wiki_de
.embset_similar(avg_de, n=1000)
.score_similar(-diff_de, n=10))
politik and demokratie are “gesellschaft” words, not “gemeinschaft” words.
# backing up - what are the words most similar to gemeinschaft overall?
emb_wiki_de.score_similar('gemeinschaft', n=50)
I notice lots of adjectives? It might be better if words were stemmed… I see e.g. gemeinschaftlich, gemeinschaftliche, gemeinschaftlichen.
One key takeaway: apparently, under this model, gesellschaft is the most similar word to gemeinschaft.
Except for “nachbarschaftlichen” I don’t see the same local connotations that “community” has in English?
TODO: Train a word2vec model on Tönnies¶
What results would I get if I train a model on a classical sociological text?
This corpus explorer is pretty sweet: http://voyant-tools.org/?view=corpusset&stopList=stop.de.german.txt&input=http://www.deutschestextarchiv.de/book/download_lemmaxml/toennies_gemeinschaft_1887
But how do I get that lemmatized text into python?
https://weblicht.sfs.uni-tuebingen.de/weblichtwiki/index.php/The_TCF_Format